|
| |
|
Contents
|
TAS, BASE,
mate, comate, global TAS, local
TAS, TAS-Code, intrinsic TAS, extrinsic TAS, closed TAS , open TAS,
|
| See also |
TOC,
AOP
Theorems
|
|
Abstract
|
Introduction
|
Priority
|
Unary
|
Prioritors
|
Operations
|
|
TAS
|
Theorems
|
Orthogonal
|
Expansion
|
Image-Scaling
|
Degeneracy
|
|
Design
|
Derive
|
AOP Versus
|
Tables
|
Figures
|
Proofs
|
|
Computer
|
Bibliography
|
|
|
|
|
 AOP TAS systems
In the previous section we presented the
prioritors of AOP. These prioritors form a complete family that has algebraic relations and rules that show how they can be used in digital circuits design. It is very important to find out these relations to enable us design MVL circuits using all prioritors.
Assume we are
going to pick a pair of two prioritors, out of the family, to determine all algebraic relations that may exist between the two prioritors in the pair. How many pairs can we generate? There are z!2 pairs of prioritors in a z-radix system.
|
For example,
The figure to the right shows all possible pairs in ternary system. Lines
show pairs of different prioritors and circles show pairs of the same prioritor.
For example, Line "12" (in red) shows the (T1,T2) pair
and line "36" (in green) shows the pair (T3,T6).
Circle "11" shows the {T1,T1) pair and circle "55"
shows the pair (T5,T5). So, the number of pairs is z!2=3!2=36. |
 |
AOP partitions these pairs into z!
groups (sets), where each group is called a TAS (Two-Operational Algebraic System) and each TAS has z! pairs. Thus, we say that AOP has z! TAS systems. For example, there are 2 TAS systems in binary system, 6 in ternary system and 24 in quaternary system.
Mathematically, a TAS is a relation on PxP where P is the set of
prioritors.
Definitions, Notations and Terminology
A TAS is defined mathematically as the set of all pairs (two prioritors) in the form of (a,b)
where ' a' is a prioritor, b=p¾a
and 'p' is a conservative unary operator called TAS BASE. Each TAS has a unique base and thus it is identified by its base where the maximum number
of bases is z!. The figure below shows a graphical illustrations where
prioritors are shown in the yellow circle, pairs are in the red circle and the pair
syntax in the green circle. Each group of z! pairs is a TAS. TASes
are represented as rings with different colors to form a cylinder. All of
these TASes represent the complete system of AOP.
For any prioritor, say a, that belongs to a TAS there exists a mate (or priomate) denoted by a!
(read as mate of a)
and is defined as <a,p>=a!=p─a
where "<>" and "!" are called the mate operators. Thus the (a,a!) pairs belong to one TAS system.
For any prioritor that belongs to a TAS system there is a conservative unary operator called a comate (or priocomate) denoted by a?
and is defined as [a,p]=a?=a-─a!
(read as comate of a)
where "[]" and "?" are called the comate operators.
If the base of a TAS is equal to the Up-Del unary operator we call it the STAR TAS (STAS) system.
In each z-radix system there is one STAS system.
If the base of a TAS is equal to the Down-Del unary operator then the TAS is called an intrinsic TAS system
(ITAS). In each z-radix system there is one ITAS system.
If the base of a TAS is equal to the Down-Del unary operator then the TAS is called an intrinsic TAS system (ITAS) otherwise it is called an extrinsic TAS system. In each z-radix system there is one intrinsic TAS system that describes the intrinsic properties of
prioritors and (z!-1) extrinsic TAS systems..
Any pair of prioritors, say (a,b),
belongs to a unique TAS whose base is given by p=b─a-.
Each pair of prioritors has a transpose pair. If (a,b)
is a pair of prioritors, then its transpose is (b,a).
The transpose of a pair is obtained by switching its components.
TAS systems are classified into open and closed TAS systems. A
closed TAS is a TAS that contains all transposes of its pairs. An open TAS is a TAS that does not contain all transposes of its pairs.
The number of closed TAS systems is equal to the number of self-inverse unary operators in the system and the number of
open TAS systems is equal to the number of none self-inverse unary operators.
When a TAS system exists in all radices it is called a global TAS and when it exists in some and not in the others it is called a local TAS.
The ITAS and STAS systems are global TAS systems and all other TAS systems are local TAS systems. Thus,
the number of global TAS systems in any z-radix digital system is 2 and local TAS systems is
(z!-2). The binary system has no local TAS systems at all. The properties of Local TAS systems serve as a selecting factor of one radix over the other.
The OTAS (Other TAS) systems is used to
refer to all TAS systems other than the ITAS and STAS systems. LTAS
is also used to refer to all local TAS systems. So, OTAS and LTAS words
have the same meaning. The number of OTAS/LTAS systems in z-radix digital
system is given by (z!-2).
AOP identifies TAS systems by the s-code and by a serial code. The serial code uses an alphanumeric index starts form "1...A...Z" determined by the order of the TAS base in a sorted list of bases based on their numerical order prefixed by 'TASc' where 'c' is a character that identifies the radix in use. For
example, 'TASQ7" is a quaternary TAS system and with an s-code of 4S1023. (Note: the 4S1023 has an alphanumeric order of '7').
Table-1  shows the TAS systems in binary system.
The two TAS systems are TASB1 and TASB2. TASB1 is an extrinsic TAS, which shows
the relations between the B1 (AND) and B2 (OR) prioritors. TASB2 is an intrinsic
TAS which shows the properties of prioritors B1 (AND) and B2 (OR).
Table-2 shows the TAS systems in ternary system.
There are six TAS systems, which are TAST1, TAST2, TAST3, TAS4, TAST5 and TAST6.
The ternary system has four closed TASes and two open TASes. Each TAS has an
independent set of equations, which describes its pairs. The operator
listed beside each TAS is the comate unary operator. For example, the comate for
the (T3,T5) pair in TAST1 is 'T4".
For example, the TAST1 TAS has 6-pairs which are (T1,T6), (T2,T4), (T3,T5),
(T4,T2), (T5,T3), and (T6,T1). We also, refer to TAST1 as the STAS system
because its base is equal to the up-del operator.
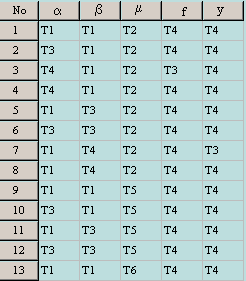
| The multiplication operation in the ternary system is given by AOP equation as
A*B=(AaB─f)m
(A─ ybB).
This
equation has 13 solutions as shown to right. To work with this circuit we
have to have full information in all ternary TAS systems. For
example, solution-1 is from TAST5, solution-6 is from TAST3, solution-9 is from
TAST2 and solution-12 is from TAST1. Once we know all the equations that govern
each TAS we can work much easily with the circuit in terms of minimizations and
understandings. See Design Example. |
 |
The intrinsic and extrinsic properties of
prioritors serve as the THEOREMS OF AOP. In the next section, we will
present the theorems of AOP that are related to ITAS and STAS systems only. A
few virtual theorems will be presented for some of OTAS systems.
|
