|
| |
 2-
THE UNIFORM DEGENERACY IN AOP 2-
THE UNIFORM DEGENERACY IN AOP
 2.1
Definitions and Notations 2.1
Definitions and Notations
The following AOP
notation will be used in the following sections. In mathematics, we usually consider variables to be the only
parameters of functions. Thus, we
specify these variables in the function heading. For example, the f(x) notation means x is a variable
parameter and the f(x,y) means x and y are variable parameters. Because AOP is a multi-operational algebra, we extend the
notation to specify variables, operators and constants as parameters
in the function heading and at the same time use sets notations to
specify such parameters. For
example, assume we have the following function in Boolean algebra G(A,B,C)= (A+B)*(A+B)+A*C+(1+C)*(B+0).
In AOP, we write this as G(X,a,C)
where X={A,B,C},a={+,*},
C={1,0}. Thus, in G(x,a,c)
notation (1) x is the set of all variables used in the function. (2) a
is the set of all prioritors used in the function. (3) C is the set of all
constants used in the function. (4) G A function whose range is determined
by a set of variables 'x' and a set of prioritors 'a'
and a set of constants 'c'.
 A
function is said to be a priority function if and only if all of its binary
operators are prioritors. A
function is said to be a priority function if and only if all of its binary
operators are prioritors.
 Definition
2.1.2 Priority Equation: An
equation is said to be a priority equation if and only if all of its binary
operators are prioritors. Definition
2.1.2 Priority Equation: An
equation is said to be a priority equation if and only if all of its binary
operators are prioritors.
 2.2 Uniform
Degeneracy of Prioritors 2.2 Uniform
Degeneracy of Prioritors
Based on the "duality" concept, in Boolean and in Post
algebras, we say that the dual of MIN is MAX and the dual of AND is OR and vise
versa. AOP extends the duality concept into a broader scope under the concept of
"uniform degeneracy[1]".
The uniform degeneracy of prioritors is defined in Definition 2.2.1
 Definition
2.2.1: The uniform degeneracy of a prioritor is defined as the image of its
priority-assignment under a conservative unary operator, say f, and is
denoted by "aofff".
Mathematically, Definition
2.2.1: The uniform degeneracy of a prioritor is defined as the image of its
priority-assignment under a conservative unary operator, say f, and is
denoted by "aofff".
Mathematically,
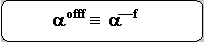
where aฏf
is the image of the priority-assignment of a
under f NOT the image of the function table of a
under f and offf is called the uniform
degeneracy operator.
 For example, let a=Q7=4S1023
and f=4S1023. By Definition-2.2.1, aofff
= 4S1023ฏ4S1023=
4S2301=QH.
Thus, we say that the uniform degeneracy of a=Q7
is QH. For example, let a=Q7=4S1023
and f=4S1023. By Definition-2.2.1, aofff
= 4S1023ฏ4S1023=
4S2301=QH.
Thus, we say that the uniform degeneracy of a=Q7
is QH.
 Table-1 Table-1
 lists all the aofff
uniform degeneracy operations of all prioritors under all conservative unary
operators in the quaternary, ternary and binary systems. To find the uniform degeneracy of a prioritor under a conservative
unary operator using
Table-1 lists all the aofff
uniform degeneracy operations of all prioritors under all conservative unary
operators in the quaternary, ternary and binary systems. To find the uniform degeneracy of a prioritor under a conservative
unary operator using
Table-1  , locate the row that contains the prioritor
and the column that contains the conservative unary operator,
which is listed in a vertical direction. The intersection of the column and row
is the prioritor number that represents the uniform degeneracy. If the number is
in the quaternary system, then add the Q prefix; in the ternary system add
the T prefix, in the binary system add the B prefix. Finally, use
Table-1 to determine the function table of the prioritor found. , locate the row that contains the prioritor
and the column that contains the conservative unary operator,
which is listed in a vertical direction. The intersection of the column and row
is the prioritor number that represents the uniform degeneracy. If the number is
in the quaternary system, then add the Q prefix; in the ternary system add
the T prefix, in the binary system add the B prefix. Finally, use
Table-1 to determine the function table of the prioritor found.
 The
uniform degeneracy under f=4S3021 of a=QH prioritor is QHofff=Q5 (The intersection is 5 and
the prefix is Q). The uniform degeneracy under f=3S021 of a=T3
prioritor is T3offf=T6
(The intersection is 6 and the prefix is T). The uniform
degeneracy under f=2S01 of a=B1 prioritor is B1offf=B2. (The intersections 2 and
the prefix is B). The
uniform degeneracy under f=4S3021 of a=QH prioritor is QHofff=Q5 (The intersection is 5 and
the prefix is Q). The uniform degeneracy under f=3S021 of a=T3
prioritor is T3offf=T6
(The intersection is 6 and the prefix is T). The uniform
degeneracy under f=2S01 of a=B1 prioritor is B1offf=B2. (The intersections 2 and
the prefix is B).
 The
uniform degeneracy of a=Q1
(MIN) under f=4S2301 is Q1offf=Q8,
of a=Q1
(MIN) under f=4S0123 is Q1offf=QO,
of a=QO
(MAX) under f=4S0123 is QOofff=Q1
and of a=Q1
(MIN) under f=4S1032 is Q1offf=QH. The
uniform degeneracy of a=Q1
(MIN) under f=4S2301 is Q1offf=Q8,
of a=Q1
(MIN) under f=4S0123 is Q1offf=QO,
of a=QO
(MAX) under f=4S0123 is QOofff=Q1
and of a=Q1
(MIN) under f=4S1032 is Q1offf=QH.
 Example-2.2.4
On Uniform Degeneracy Table: In the
binary system, under f=2S01, the uniform degeneracy of the AND operator (B1)
is the OR operator (B2) and the uniform
degeneracy of the OR operator (B2) is the
AND operator (B1). That is ANDofff=OR
and ORofff=AND. Example-2.2.4
On Uniform Degeneracy Table: In the
binary system, under f=2S01, the uniform degeneracy of the AND operator (B1)
is the OR operator (B2) and the uniform
degeneracy of the OR operator (B2) is the
AND operator (B1). That is ANDofff=OR
and ORofff=AND.
 The duality theory is a special case of the
uniform degeneracy theory of AOP. The dual operation in Boolean and
Post algebras is the uniform degeneracy under the D
conservative operator. For example, in the quaternary system f=D=4S0123
and MIN=Q1=4S0123, thus the dual of MIN is
MINofff=4S0123พ4S0123=
4S3210=QO=MAX. In the binary system f=D=2S01,
thus the dual of AND is ANDofff=2S01พ
2S01=2S10=OR.
The duality theory is a special case of the
uniform degeneracy theory of AOP. The dual operation in Boolean and
Post algebras is the uniform degeneracy under the D
conservative operator. For example, in the quaternary system f=D=4S0123
and MIN=Q1=4S0123, thus the dual of MIN is
MINofff=4S0123พ4S0123=
4S3210=QO=MAX. In the binary system f=D=2S01,
thus the dual of AND is ANDofff=2S01พ
2S01=2S10=OR.
 2.4
Uniform Degeneracy of
Priority Functions 2.4
Uniform Degeneracy of
Priority Functions
The
duality of functions in Boolean and Post algebras is extended by AOP under the
concept of "uniform degeneracy of functions" as defined by
Definition 2.4.1.
 Definition
2.4.1: The uniform degeneracy of a priority function, say G(x,a,c)
, under a conservative unary operator, say f, is obtained by
taking the uniform degeneracy of each prioritor in the function and by taking
the image of each constant using the f conservative operator where the
variables of the function remain unchanged. Mathematically Definition
2.4.1: The uniform degeneracy of a priority function, say G(x,a,c)
, under a conservative unary operator, say f, is obtained by
taking the uniform degeneracy of each prioritor in the function and by taking
the image of each constant using the f conservative operator where the
variables of the function remain unchanged. Mathematically
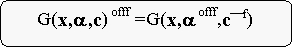
The expression G(x,a,C)offf
is read
as the uniform degeneracy of the function G. According to
Definition-2.4.1, we have to take the uniform degeneracy of each prioritor and
take the image of each constant and leave all variables untouched. The statement
is translated symbolically as G(X,aofff,C─f).
This means that the "offf " uniform degeneracy
is to operate on all the prioritors of the set 'a'
and the '─f' image operator is to operate on all the constants of the set
'C'.
For example, let G(X,a,C)=
(A+B)*(A+B)+A*C+(1+C)*(B+0) where x={A,B,C},a={+,*},
and C={1,0}. Using the uniform
degeneracy definition, G(A,B,C)offf=G(X,aofff,C─f)=
G({A,B,C},{+,*}offf,{1,0}─f)=
G({A,B,C},{+offf,*offf},{1─f,0─f})=
(A+offf
B)* offf
(A+offf
B)+ offf
A* offf
C+offf
(1─f +offf
C)* offf
(B+offf
0─f
 Example-1: Let
a=Q1
(MIN) in the quaternary system and let g(X,a,C)=Aa(2a*B).
The set of all variables in the function is X={A,
B}, the set of all constants in the function is
C={2}, and the set of all prioritors is a={a, a*}. The offf uniform degeneracy of g(X,a,C)
is given by g(X,a,C)offf=A
aofff(2─f a*offf
B). In this example, we took the uniform
degeneracy of each prioritor and took the image of the constant '2'. If we let
f=4S0123, we get g(X,a,C)offf=A
MAX
(1 MIN
B) or g(X,a,C)offf=A+(1ทB)=AÚ
(1ÙB)
using Boolean and Post notations. Example-1: Let
a=Q1
(MIN) in the quaternary system and let g(X,a,C)=Aa(2a*B).
The set of all variables in the function is X={A,
B}, the set of all constants in the function is
C={2}, and the set of all prioritors is a={a, a*}. The offf uniform degeneracy of g(X,a,C)
is given by g(X,a,C)offf=A
aofff(2─f a*offf
B). In this example, we took the uniform
degeneracy of each prioritor and took the image of the constant '2'. If we let
f=4S0123, we get g(X,a,C)offf=A
MAX
(1 MIN
B) or g(X,a,C)offf=A+(1ทB)=AÚ
(1ÙB)
using Boolean and Post notations.
 Let
g(X,a,C)=Aa(Ba*C). The offf uniform degeneracy of g(X,a,C)
is g(X,a,C)offf=A
aofff(Ba*offf
C). This
example dose not have constants. Let
g(X,a,C)=Aa(Ba*C). The offf uniform degeneracy of g(X,a,C)
is g(X,a,C)offf=A
aofff(Ba*offf
C). This
example dose not have constants.
 Example-3: Let
a=Q1=MIN
in the quaternary system and let g(X,a,C)=(Aa(2a*B)a(Ca*3))a*(0aC). The offf uniform degeneracy of g(X,a,C)
is given by g(X,a,C)offf=(Aaofff(2─fofff(Ca*offf
3─fofffC). Example-3: Let
a=Q1=MIN
in the quaternary system and let g(X,a,C)=(Aa(2a*B)a(Ca*3))a*(0aC). The offf uniform degeneracy of g(X,a,C)
is given by g(X,a,C)offf=(Aaofff(2─fofff(Ca*offf
3─fofffC).
If f=4S1302, we obtain g(X,a,C)offf=(AQE(3QBB)QE(CQB1))QB(2QEC).
Note that aofff=
Q1offf=4S0123─4S1302=
4S2031=QE and a*offf=QOofff=MAXofff=4S3210─4S1302=4S1302=QB.
Theorem-2.4.1
shows another important theorem in AOP. This
theorem gives us another way of obtaining the uniform degeneracy without using
Definition-2.4.1.
 Theorem 2.4.1 Uniform Degeneracy Equivalence
Theorem Theorem 2.4.1 Uniform Degeneracy Equivalence
Theorem
The uniform
degeneracy of a priority function, say G(x,a.c), under offf
, where f is a conservative unary operator, is equivalent to taking the
image of the entire function and the inverse image of each variable in the
function. Mathematically:
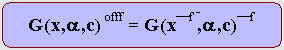
 Example-4: Let
g(X,a,C)=Aa(Ba*C). Example-4: Let
g(X,a,C)=Aa(Ba*C). 
Let
g(X,a,C)=Aa(2a*C).

 2.5
Uniform Degeneracy of Priority
Equations 2.5
Uniform Degeneracy of Priority
Equations
The
duality theory in Boolean and Post algebras shows us how to obtain
the dual of equations. In Boolean algebra, the dual of an equation is obtained by substituting
an AND for OR, an OR for AND, 0 for 1 and 1 for 0. In Post algebra, the dual of
an equation is obtained by substituting a MIN for MAX, a MAX for MIN, 0 for u
and u for 0 [5]. According to this theory, there is a dual for
every equation in Boolean and Post algebras. AOP extends the duality theory into
a new theory (Theorem-2.5.1) called Equations Uniform Degeneracy
Theorem. This new theory tells us that each MVL equation has z!
degenerate forms. It simply states, "give me a MVL equation and I will
generate for you z! equations". For example, we can generate 24
equations from a MVL equation in the quaternary system by AOP (see
Example-2.5.3) but on the other hand we can generate only two equations by Post
algebra. AOP in this example extends the number of equations to 24 equations .
 Theorem 2.5.1 Equations Uniform Degeneracy Theorem: Theorem 2.5.1 Equations Uniform Degeneracy Theorem:
The uniform
degeneracy of both sides of a priority equation in a z-radix digital
system are equal and the number of uniformly degenerate equations is
equal to z!. That is, if G(x,c,a)=H(x,c,a) then G(x,c,a)offf
= H(x,c,a)offf
 Example-2.5.1 In
Boolean algebra the dual of A+(B+1)=1
is Aท(Bท0)=0. In AOP, the uniform degeneracy of A+(B+1)=1 under the unary
f=2S01 (NOT) is A+offf(B+offf
1─f)=1─f . Using Table-1,
+offf=B2offf=B1=AND=ท
and 1─f =0, we get Aท(Bท0)=0, which is the same result obtained by the dual operation. Example-2.5.1 In
Boolean algebra the dual of A+(B+1)=1
is Aท(Bท0)=0. In AOP, the uniform degeneracy of A+(B+1)=1 under the unary
f=2S01 (NOT) is A+offf(B+offf
1─f)=1─f . Using Table-1,
+offf=B2offf=B1=AND=ท
and 1─f =0, we get Aท(Bท0)=0, which is the same result obtained by the dual operation.
 In the
quaternary system, let a=Q1
=MIN. The uniform degeneracy of the 2a
(Ba*C)=(2aB)
a*(2aC) MVL equation is given by 2─f
aofff(Ba*offfC)=(
2─f
aofff
B) a*offf(2─f
aofffC).
If f=4S2301, then we obtain 3Q8(BQHC)=(
3Q8B)QH(3Q8C).
Note that the Q8 and
QH
form a STAS system that satisfies the distribution theorem. Also, note that aofff=Q1offf=4S0123─4S2301=4S1032=Q8
and a*offf=QOofff=
MAXofff=4S3210─4S2301=4S2301=QH. In the
quaternary system, let a=Q1
=MIN. The uniform degeneracy of the 2a
(Ba*C)=(2aB)
a*(2aC) MVL equation is given by 2─f
aofff(Ba*offfC)=(
2─f
aofff
B) a*offf(2─f
aofffC).
If f=4S2301, then we obtain 3Q8(BQHC)=(
3Q8B)QH(3Q8C).
Note that the Q8 and
QH
form a STAS system that satisfies the distribution theorem. Also, note that aofff=Q1offf=4S0123─4S2301=4S1032=Q8
and a*offf=QOofff=
MAXofff=4S3210─4S2301=4S2301=QH.
 Given
this equation "AÙ(BÚC)=(AÙB)Ú(AÙC)"
in Post notation, give all the 24 degenerate equations in the quaternary system
where Ù=MIN
and Ú=MAX.
Using AOP notation, we can express AÙ(BÚC)=(AÙB)Ú(AÙC)
as Aa1
(B aOC)=(A a1B)
aO(A
a1C)
where Ù=MIN=Q1
, Ú=MAX=
QO. The 24 degenerate equations are listed
in Table-5. The index of each a
represents the prioritor number as listed in Table-1.
For example, a7=Q7,
aM=QM
etc. Note that the 24 uniform degeneracy operators are obtained directly from
Table-3 by picking all the prioritors in a row. For example, for the z!
degeneracy forms of Q1 we pick its row in
Table-3 which reads "OIMCGA-NHK6E4-LBJ582-F9D371" and the same
for QO which reads "123456-789ABC-DEFGHI-JKLMNO".
Note that the first equation is the dual of the given equation in
Post algebra. This shows that the
dual operation in Boolean and Post algebras is equivalent to the uniform
degeneracy under the D
operator. Also, note that equation
No 24 is equal to the given equation, because the uniform degeneracy of any
equation under the Ñ
operator is equal to the equation itself. Given
this equation "AÙ(BÚC)=(AÙB)Ú(AÙC)"
in Post notation, give all the 24 degenerate equations in the quaternary system
where Ù=MIN
and Ú=MAX.
Using AOP notation, we can express AÙ(BÚC)=(AÙB)Ú(AÙC)
as Aa1
(B aOC)=(A a1B)
aO(A
a1C)
where Ù=MIN=Q1
, Ú=MAX=
QO. The 24 degenerate equations are listed
in Table-5. The index of each a
represents the prioritor number as listed in Table-1.
For example, a7=Q7,
aM=QM
etc. Note that the 24 uniform degeneracy operators are obtained directly from
Table-3 by picking all the prioritors in a row. For example, for the z!
degeneracy forms of Q1 we pick its row in
Table-3 which reads "OIMCGA-NHK6E4-LBJ582-F9D371" and the same
for QO which reads "123456-789ABC-DEFGHI-JKLMNO".
Note that the first equation is the dual of the given equation in
Post algebra. This shows that the
dual operation in Boolean and Post algebras is equivalent to the uniform
degeneracy under the D
operator. Also, note that equation
No 24 is equal to the given equation, because the uniform degeneracy of any
equation under the Ñ
operator is equal to the equation itself.

|