|
| |
 REPRESENTATIONS OF MVL FUNCTIONS IN AOP REPRESENTATIONS OF MVL FUNCTIONS IN AOP
Boolean and Post algebras offer only two representations for n-variable
MVL functions: sum-of-products and product-of-sums [5]
p29-30 [9] p.95. Each representation requires a maximum number of (n+1)zn-1 binary operations (MIN-MAX, AND-OR) and a maximum number of nzn
complementary functions {Cm(x) [5]}. For example, for a
two- variable function in the ternary system we need a maximum number of (2+1)32-1=26
binary operations {8 MINs & 18 MAXs or 8 MAXs & 18 MINs [8]p.93}
and 2*32=18
complementary functions.
AOP
extends and enhances the representations of MVL functions. It offers z! distinct
representations for MVL functions instead of two
representations. The sum-of-products and product-of-sums representations are
just two representations out of the z! distinct representations. For example, a
MVL function in the quaternary system can be represented by 4!=24
representations. AOP extends the representations of MVL functions using two
theorems called “Orthogonal Theorem-I” and “Orthogonal
Theorem-II”. Both theorems extend the number of representations of MVL
functions to z!. The z! distinct representations give designers more alternate
choices of representing MVL functions. It also enables designers to select the
representation which starts-off with the lowest number of prioritors just
before entering the minimization dilemma.
AOP
enhances the notations of MVL function representations. Its notations allow the
use of well-organized and compact formulas that handle hundreds of
representations in high-radix systems. Before we present the orthogonal theorems
of AOP, we will consider the following notation, terminology, and symbols.

 3.1 Notations, Terminology, Symbols
and Definitions 3.1 Notations, Terminology, Symbols
and Definitions
In AOP, the domain of MVL functions is treated as a vector domain with zn
vectors. The notation f(un,...,u2,u1)
is written as f(XS) where Xs=(Xsn,...,XS2,XS1)
and 's' is the vector index in the domain. The values of the vector component XSj
correspond to the values of the uj variables where 1£j£n.
 TERMINOLOGY
In AOP, some of the values in the function table
are called "trivial values". A trivial value is the value that
is equal to the supremum of the prioritor used to represent its function. A
term is all the repeated operations carried out by the a
prioritor in the representation. A term is called a trivial term if a
trivial value appears in it. If there are no trivial terms in the final
representation, then we call it a start-off representation. MRV is the most repeated
value in the function table. NMRV is the next most
repeated value in the function table. TERMINOLOGY
In AOP, some of the values in the function table
are called "trivial values". A trivial value is the value that
is equal to the supremum of the prioritor used to represent its function. A
term is all the repeated operations carried out by the a
prioritor in the representation. A term is called a trivial term if a
trivial value appears in it. If there are no trivial terms in the final
representation, then we call it a start-off representation. MRV is the most repeated
value in the function table. NMRV is the next most
repeated value in the function table.
 SYMBOLS The following symbols
are used in the statistical theorems associated with the orthogonal theorems
I&II. (1) 'A' is the number of a's in the representation. (2) 'd' is the number of a*'s in the representation. (3) 'p' is the total
number of prioritors in the representation. (4) 't' is the number of trivial
terms in the function to be represented (5) ‘t’
is the number of none trivial terms in the equation. (6) j is the number of orthogonal operators. SYMBOLS The following symbols
are used in the statistical theorems associated with the orthogonal theorems
I&II. (1) 'A' is the number of a's in the representation. (2) 'd' is the number of a*'s in the representation. (3) 'p' is the total
number of prioritors in the representation. (4) 't' is the number of trivial
terms in the function to be represented (5) ‘t’
is the number of none trivial terms in the equation. (6) j is the number of orthogonal operators.
 Definitions Definitions
In
AOP, we face situations where we have to count the number of occurrences of a
digit in the range set of a MVL function. The next definition defines a counter
operator which is used to expresses the mathematical formulas of AOP in a
well-compact form.
 Definition
3.1.1 Counting Operator: Let
“A” be a subset of the integer numbers and let 'c' be an integer number. The
expression A#c is
defined as the number of occurrences of the 'c' element in the A set where
"#" is called the counting operator. Definition
3.1.1 Counting Operator: Let
“A” be a subset of the integer numbers and let 'c' be an integer number. The
expression A#c is
defined as the number of occurrences of the 'c' element in the A set where
"#" is called the counting operator.
Example-3.1
Counting Operator: Let f(A, B)=
AbB
be a function in the quaternary system where b=Q8=4S1032=4S3310:3210:1111:0010.
The expression {f(A, B)}#2
=is the number of the occurrences of '2' in the function range set which is '1'.
For simplicity in notations, we will treat the function symbol 'f' under the counting
operator as its range set and disuse the parenthesis. Thus f#0=5,
f#1=7,
f
#2=1, f#3=3.

 3.2
Orthogonal Theorem-I 3.2
Orthogonal Theorem-I
AOP
uses the orthogonal theorem-I (Theorem 3.2.1) to represent MVL functions. The
orthogonal theorem-I requires a maximum number of (n+1)zn-1
prioritors and a maximum number of nzn
orthogonal operators. For example, a 2-variables MVL function in the ternary
system can be represented by six representations with a maximum number of 26
prioritors and 18 orthogonal operators for each representation. The
sum-of-products and product-of-sums [5] p29-30 [9]p.95 representations of Post algebras are special cases of
the orthogonal-I representations. Therefore, they require a
maximum number of (n+1)zn-1
MINs and MAXs and a maximum number of nzn
complementary
operators [5].
Theorem 3.2.2 shows statistical formulas for the
representations obtained by orthogonal theorem-I. The theorem uses the counting operator defined in
Definition-3.1.1
 Theorem 3.2.1 Orthogonal Theorem-I: A MVL function of n-variables, say f(xs)
where XS=(XSn,
..., XS2,
XS1),
can be represented by using the (a,
a*)
STAS systems and the unary orthogonal operators as: Theorem 3.2.1 Orthogonal Theorem-I: A MVL function of n-variables, say f(xs)
where XS=(XSn,
..., XS2,
XS1),
can be represented by using the (a,
a*)
STAS systems and the unary orthogonal operators as:
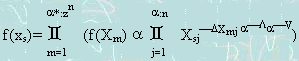
|
|
 Theorem 3.2.2 Statistics in Orthogonal Theorem-I Theorem 3.2.2 Statistics in Orthogonal Theorem-I
1- The number of trivial
terms is ………….. t=
F#a¾L
2- The number of none trivial terms is ……..t=zn-t
3- The number of orthogonal operators is
j=nt
4- The number of a*’s
is …………………..d=t-1
5- The number of a’s
is
……………………A=nt-F#a¾V
6- The total number of prioritors is …P=A+d=(n+1)t-1-F#a¾V
|
The Post representations are a special
case of orthogonal theorem-I when a=MIN
for the sum-of-products representation and when a=MAX
for the product-of-sums representation.

 3.3
Orthogonal Theorem-II 3.3
Orthogonal Theorem-II
AOP
enhances the representations of MVL functions by the orthogonal theorem-II
(Theorem 3.3.1). The enhancement is achieved by reducing the number of
prioritors needed for the representations of MVL functions than the orthogonal-I
representations by zn
. This makes the orthogonal-II representations less
complex than the orthogonal-I representations. The orthogonal theorem-II
requires a maximum number of nZn-1 prioritors
and a maximum number of nzn
orthogonal operators. For example, a 2-variables MVL
function in the ternary system can be represented by six representations using
the orthogonal theorem-II with a maximum number of 17 prioritors and 18
orthogonal operators (see Example-3.4.1; the MIN and MAX are prioritors).
Post
algebra does not have an equivalent theorem to the orthogonal theorem-II.
Therefore, the orthogonal-II representations of AOP to MVL functions are less
complex than Post representations by a maximum number of Zn
binary operations.
|
 Theorem
3.3.1 Orthogonal Theorem-II: A
MVL function with n-variables, say f(xs)
where XS=(XSn,
..., XS2,
XS1),
can be represented by using the (a,
a*)
STAS systems and the unary orthogonal operators as: Theorem
3.3.1 Orthogonal Theorem-II: A
MVL function with n-variables, say f(xs)
where XS=(XSn,
..., XS2,
XS1),
can be represented by using the (a,
a*)
STAS systems and the unary orthogonal operators as:

|
|
 Theorem 3.3.2 Statistics in Orthogonal Theorem-II
Theorem 3.3.2 Statistics in Orthogonal Theorem-II
1- The number of trivial terms is ………….. t=
F#a¾L
2- The number of none trivial terms is ….….t=zn-t
3- The number of orthogonal operators is …j=nt
4- The number of a*’s
is ………………..….d=t-1
5- The number of a’s
is
……………………A=(n-1)t
6- The total number of prioritors is … ……....P=A+d
=nt-1
|

 MVL functions representations in AOP
MVL functions representations in AOP
How
AOP represents a MVL function if given a STAS system?
In this case, we do the followings steps: (1) Delete all entries in the function
table which are equal to a¾
L (2) Select orthogonal theorem I or II for the
representation. (3) Mark all entries in the function table that are equal to a¾
V if orthogonal theorem-I was selected. (4) Transfer
the function table into the selected orthogonal theorem as shown in
Example-3.4.2 and Table-6.
 How
AOP represents a MVL function if not given a STAS system? In this
case, we do the following steps to get the lowest
start-off representation (Definition-3.4.1). (1)
Find the MRV and NMRV from the function
table. (2) Select a prioritor from Table-1, say a,
such that a¾
L=MRV and a¾
V=NMRV. (3) Delete all entries in the function table
which are equal to the function MRV (4) Select orthogonal theorem I or II for
the representation. (5) Mark all entries in the function table that are equal to
the function NMRV if orthogonal theorem-I was selected. (6) Transfer the
function table content into the selected orthogonal theorem. The marked values
will not appear in the orthogonal-I representations because they are the infimum
of a
and are irrelevant to the orthogonal-II representation. See Example-3.4.2
and Table-6: How
AOP represents a MVL function if not given a STAS system? In this
case, we do the following steps to get the lowest
start-off representation (Definition-3.4.1). (1)
Find the MRV and NMRV from the function
table. (2) Select a prioritor from Table-1, say a,
such that a¾
L=MRV and a¾
V=NMRV. (3) Delete all entries in the function table
which are equal to the function MRV (4) Select orthogonal theorem I or II for
the representation. (5) Mark all entries in the function table that are equal to
the function NMRV if orthogonal theorem-I was selected. (6) Transfer the
function table content into the selected orthogonal theorem. The marked values
will not appear in the orthogonal-I representations because they are the infimum
of a
and are irrelevant to the orthogonal-II representation. See Example-3.4.2
and Table-6:

 Lowest Start-Off
Representation Lowest Start-Off
Representation
The
lowest start-off representation does not mean the minimum representation.
Further steps have to be carried by the theorems of AOP to get a minimum
representation.
 Definition
3.4.1 Lowest Start-Off Representation: A representation is called the
lowest start-off representation if
the supremum of the prioritor used to represent the function is equal to its MRV
and the infimum is equal to its NMRV. That is a¾
L=MRV, a¾
V=NMRV. Definition
3.4.1 Lowest Start-Off Representation: A representation is called the
lowest start-off representation if
the supremum of the prioritor used to represent the function is equal to its MRV
and the infimum is equal to its NMRV. That is a¾
L=MRV, a¾
V=NMRV.

 Examples of MVL
functions Examples of MVL
functions
In [8] p. 92-93 the ternary
function example f(u,v) is represented by the sum-of-products in p.93. Let's
represent the example using the orthogonal theorem-II of AOP. From H1, we get a=Ù=·=MIN,
a*=Ú=+=MAX,
and the logic-set={e0, e1,
e2}. From H2, by the infimum theorem a¾
V=e2,
a*¾
V=e0, by the star-cyclic
theorem a¾L=a*¾
V=e0
and a*¾
L=a¾
V=e2.
Thus f(u,v) can be represented in AOP by the orthogonal theorem-II as listed
below. This representation has 9 MINs and 8 MAXs compared to
18 MINs and 8 MAXs by Post algebra.

 Example-3.4.2 Orthogonal Theorems-I&II:
Let f(u,v) in Example-3.4.1 be f(u,v)=ubv where b=T4=3S120=3S212:111:210
and the logic-set={0,1,2}. From the function table, MRV=1 and NMRV=2. Using
Table-1, we select a=T3=3S102
since T3¾
L=MRV and T3¾V=NMRV.
Thus, the representation by orthogonal theorem-I is f(u,v)=(
0au¾
D012 av¾
D012)a*(
u¾
D012 av¾
D212) a*(
u¾
D212 av¾
D012)a*(
u¾
D212 av¾
D212) with 8 binary operations and 8 orthogonal operators and no NMRV values
are appearing in the representation. The representation by orthogonal
theorem-II is
f(u,v)= (u¾
D010
av¾
D010)a*(u¾
D012
av¾
D212)a*( u¾
D212
av¾
D012)a*(u¾
D212
av¾
D212)
with 7 binary operations and 8
orthogonal operators. See Table-6. These representations can be minimized
using the theorems of AOP. For example, using the substitution theorem (Theorem
5.1.3), we reduce the last two terms and get f(u, v)=( 0au¾
D012 av¾
D012)a*(
u¾
D012 av¾
D212)a*(
u¾
D212 av¾
D121) for the orthogonal-I representation
and f(u, v)= (u¾
D010 av¾
D010)a*(u¾
D012
av¾
D212)a*( u¾
D212
av¾
D121)
for the orthogonal-II representation. Example-3.4.2 Orthogonal Theorems-I&II:
Let f(u,v) in Example-3.4.1 be f(u,v)=ubv where b=T4=3S120=3S212:111:210
and the logic-set={0,1,2}. From the function table, MRV=1 and NMRV=2. Using
Table-1, we select a=T3=3S102
since T3¾
L=MRV and T3¾V=NMRV.
Thus, the representation by orthogonal theorem-I is f(u,v)=(
0au¾
D012 av¾
D012)a*(
u¾
D012 av¾
D212) a*(
u¾
D212 av¾
D012)a*(
u¾
D212 av¾
D212) with 8 binary operations and 8 orthogonal operators and no NMRV values
are appearing in the representation. The representation by orthogonal
theorem-II is
f(u,v)= (u¾
D010
av¾
D010)a*(u¾
D012
av¾
D212)a*( u¾
D212
av¾
D012)a*(u¾
D212
av¾
D212)
with 7 binary operations and 8
orthogonal operators. See Table-6. These representations can be minimized
using the theorems of AOP. For example, using the substitution theorem (Theorem
5.1.3), we reduce the last two terms and get f(u, v)=( 0au¾
D012 av¾
D012)a*(
u¾
D012 av¾
D212)a*(
u¾
D212 av¾
D121) for the orthogonal-I representation
and f(u, v)= (u¾
D010 av¾
D010)a*(u¾
D012
av¾
D212)a*( u¾
D212
av¾
D121)
for the orthogonal-II representation.

|