In this section, I will present a simple design example to compare between the design using traditional operators and between AOP operators. Since, the major operations in our lives are the basic arithmetic operations: addition, subtraction, division and multiplication, we will provide different designs for the multiplication operation in ternary system using AOP and Post algebras and then compare the results.

1-Example-1:Ternary Multiplication Operation Design

Traditional Design
The function table for the ternary multiplication operation using s-code notation of AOP is 3S120:210:000.

Design Example-1.1: Ternary Multiplier Design using Post Algebra
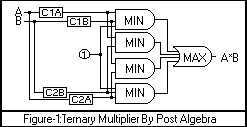
Post uses traditional operators MIN, MAX, MV-NOT, C0(x), C1(x) and C2(x). Using Post notation and its representation of functions, we get the following "sum-of-products" equation (where: *=Min, +=MAX) A*B= [1* C1(A)* C1(B) ]+ [ C1(A)*C2(B) ]+ [ C2(A)* C1(B) ]+ [1* C2(A)*C2(B) ]
This Post representation uses 9 binary operators (6 MIN, 3 MAX), and 8 unary operators (complementary functions). The corresponding circuit for this equation is shown in Figure-1.  The "product-of-sums" representation uses  15 binary operators (9 MIN,  6 MAX), and 14 unary operators (complementary functions).

In the traditional designs section we presented the design of the ternary multiplication. Let's take this operation and show its designs using AOP. The function table for the ternary multiplication operation using s-code notation of AOP is 3S120:210:000.  Before we start, here are AOP operators for ternary system.

The multi-operations used by AOP in the ternary system 1.      Conservative unary operators T1, T2, T3, T4, T5 and T6. (see Table-1) 2.        Orthogonal operators: 3W001, 3W002, 3W010, 3W012, 3W020, 3W02  ,3W101, 3W102, 3W110, 3W112, 3W120, 3W121, 3W201, 2W202, 3W210, 3W212, 3W220, 3W221 3.      Prioritors: T1, T2, T3, T4, T5 and T6. (see Table-1)

As we see, AOP has a total of 30 operations in the ternary system: 24 are unary operations (out of 33=27 unary operations of ternary system) and 6 are binary operations (out of 332=19,863 binary operations of ternary system), which are its prioritors. The traditional binary operators by AOP notations are T1 (MIN), T6 (MAX) and for unary operators are T1 (MV-NOT) , T6 (identity operator), 3W002 for C0(x), 3W102 for C1(x) and 3W202 for C2(x).

Design Example-1.2: Design using AOP Orthogonal Theorem-I
The orthogonal theorem-I is similar in format to Post representations except it is generalized to cover all the binary and unary operations of AOP. The MRV (most repeated value) in this table (3S120:210:000) is “0”. Thus we select a prioritor whose supremum-digit is equal to zero. The NMRV (next most repeated value) in this table (3S120:210:000) is ‘1’ and ‘2’. Since we have two values for NMRV, we may select a prioritor with '2' infimum-digit or with '1' infimum-digit.
The prioritor with the 1-infimum digit and 0-supremum digit is T2.  Thus, we have   a=T2, a ¾ Ù =0,  a¾ Ú =1,  a*=T4. According to this, one of the best STAS systems to represent this function which will start-off with the lowest- representation (not minimum) is (T2,T4).  On the other hand,  the prioritor with 0-supremum digit and 2-infimum digit is T1 (MIN).
Thus, a =T1, a ¾ Ù =0,  a¾ Ú =2,  a*=T6 (MAX).  According to this, one of the best STAS systems to represent this function which will start-off with the lowest-representation (not minimum) is (T1,T6).  Let's just use the (T1,T6) STAS system. By substituting in orthogonal theorem-I of AOP we get A*B= [1a A¾ D102 a B¾ D102]a *[ A¾ D102 a B¾ D202]a *[ A¾ D202 a B¾ D102]a *[1a A¾ D202 a B¾ D202] using AOP short notation we get A*B= [1a A102 a B102]a *[ A102 a B202]a *[ A202 a B102]a *[1a A202 a B202] Note that this representation by AOP for this specific example is the same as of Post. It uses 6 T1 (MIN) and 3 T6 (MAX). The corresponding circuit for this equation is shown in Figure-2 using AOP notations for circuits.

Design Example-1.3: Design using AOP Orthogonal Theorem-II
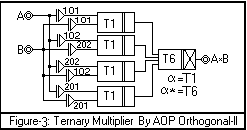
We will use the same STAS system obtained by orthogonal theorem-I, but we substitute in orthogonal theorem-II to get the following equation: A*B=[A¾  D101a B¾  D101]a*[A¾  D102a B¾  D202]a*[A¾  D202 aB¾  D102]a*[A¾ D201 a B¾  D201] using AOP short-notations we get A*B=[A101a B101]a*[A102a B202]a*[A202 aB102]a*[A201 a B201]
This representation is different from Post representation and AOP orthogonal-I representation. It uses 4 T1 (MIN) and 3 T6 (MAX). The corresponding circuit for this equation is shown in Figure-3.

Design Example-1.4: Using AOP multi-operational set of basic operators

If we were to think of a different circuit for the above example, other than the one provided by Post representation, then we would find it is impossible to use the MIN, MAX and MV-NOT to design such a circuit. Even the Post representation used the complementary functions to get the job done.

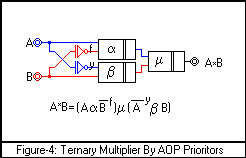
Let’s use AOP and present different designs to the same example we started with. Consider the circuit of Figure-4, which is drawn using AOP symbols for digital circuits. This circuit contains three prioritors labeled a, b, and m and two conservative unary operators labeled “f” and “y” and it represents the ternary multiplication operation.   A*B= (AaB¾f)m (A¾ ybB)
A solution to this circuit, based on AOP multi-operators set, was carried out and gave 13 distinct circuits. A few are presented in Table-1. In comparison to the previous circuits, this circuit uses three prioritors (like saying 3 MIN) and two conservative unary operators (like saying 2 complementary functions or two orthogonal operators).  Note: This circuit can be reduced to two binary operators and one unary operator using the virtual theorems of AOP. (see TAS systems)	Table-1
	No	a	b	m	"f"	"Y"
	1	T3	T3	T5	T4	T4
	2	T1	T1	T2	T4	T4
	3	T1	T4	T2	T4	T3
	4	T4	T1	T2	T4	T4
	5	T1	T1	T6	T4	T4
	6	T1	T1	T5	T4	T4
	7	T4	T1	T2	T3	T4

Decision Making: If we have to select one design from the aforementioned four examples, which one will we choose? From an engineering point of view, will use the design of Example-1.4 by AOP because it is  less complex, has low power consumption, has less propagation delay, has higher in speed, and uses les chip space than the other designs. From a managerial point of view, we will choose  the design of Example-1.4 by AOP because it is more economical in terms of cost. The Post design used used 9 binary operations 8 unary operators while the circuit of Example-1.4 (Figure-4) used three binary operators and two unary operators. This difference represents 66% reduction in cost of binary operations and 62.5% reduction in cost of ternary operations. Let's take a few of the solutions as shown in Table-1 above and discus them. In 1-11 entry, we can use T3, and T5 prioritors and T4 conservative operator. Entry 2-1 shows another configuration. It uses T1 and T2 prioritors and T4 conservative operator. This entry shows how T2 and T4 cooperate with the traditional operator T1 to get the job done. The same can be said for the other entries.  It is impossible to design this circuit of Figure-4 using the traditional operators of Post. Thus, an engineer who relies on Post representations and has a solid faith in its operators will never come up with such a circuit and will have only the circuit we obtained in  design, example-1 which is more complex.

2-Example-2: Design of 3S201:001:111

Assume we are given a two-variable function with a function table given by s-code as 3S201:001:111. First we will represent the function using Post and then using AOP.

Design Example-2.1: Design of Ternary Operation Shown in Table below
Assume we are given a two-variable function F(A,B) as shown.  Using Post notation we get the following representation (sum-of-products) F(A,B)= [1* C0(A)* C0(B) ]+ [1* C0(A)* C1(B) ]+ [1* C0(A)* C2(B) ]+ [1* C1(A)* C0(B) ]+ [1* C2(A)* C0(B) ]+ [C2(A)* C2(B) ] This representation uses 16 binary operations (11 MIN and 5 MAX) and 12 unary operations.	A~B 0 1 2 0 1 1 1 1 1 0 0 2 1 0 2
If we use the product-of sums we get the followings: F(A,B)= [1+ J0(A)+ J0(B) ]* [1+ J0(A)+ J1(B) ]* [1+ J0(A)+J2(B) ]* [1+ J1(A)+J0(B) ]* [J1(A)+ J1(B) ]*   [J1(A)+ J2(B) ]*[1+J2(A)+ J0(B) ]*[J2(A)+ J1(B) ] This product-of-sums representation uses 20 binary operations (13 MAX and 7 MIN) and 16 unary operations.

Design Example-2.2:Using Orthogonal theorem-I  

For any function, Post algebra has no choices except to represent the function by MIN, MAX and complementary functions.  But this is different in AOP.  Since AOP has multiple operations, it does the followings: it searches for the best STAS set of prioritors and then uses its orthogonal theorems to represent the function.  In ternary multiplication design, AOP selected (T1,T6) and (T2,T4) as the best STAS systems and we went on and used (T1,T6) for comparison reasons with Post.  But note the difference in this example, here AOP selects one STAS system based on the function to be represented. 

The MRV (most repeated value) in the function table (3S201:001:111) of this function is “1”, thus we select a prioritor whose supremum-digit is equal to one. The NMRV (next most repeated value) in this table is ‘0’, thus we select a prioritor with an infimum-digit equal to ‘0’. The prioritor with 1-supremum digit and 0-infimum digit is T4. Thus a =T4, a ^{¾ Ù} =1 a^{¾ Ú} =0, and a*=T2. The best STAS system to represent this function which will start-off with the lowest representation (not minimum) is (T4,T2). By substituting in AOP orthogonal theorem-I we get:

F(A,B)= [0aA^{¾ D110}aB^{¾ D110}]a*[0aA^{¾ D110}aB^{¾ D210}]a[0aA^{¾ D210}aB^{¾ D110}]a[2aA^{¾ D210} aB^{¾ D210}]  

Since 0 is the infimum digit of a , then using the infimum-theorem, we modify the first three terms and get

F(A,B)= [A^{¾ D110} a B^{¾ D110}]a*[A^{¾ D110} a B^{¾ D210}]a*[A^{¾ D210} a B^{¾ D110}]a*[2a A^{¾ D 210}aB^{¾ D 210}]

using AOP short-notations we get

F(A,B)= [A¹¹⁰ a B¹¹⁰]a*[A¹¹⁰ a B²¹⁰]a*[A²¹⁰ a B¹¹⁰]a*[2a A²¹⁰aB²¹⁰]

This representation uses 5 T4s, 3 T3s, and 8 orthogonal operators. That is a total of 8 prioritors (8 binary operations) and 8 orthogonal operators. However, the Post representation for the same function by sum-of-products used 16 binary operations and 12 complementary functions and by product-of-sums it used 20 binary operations and 16 unary operations.  The difference between the representations of AOP and Post is 8 binary operations plus 4 unary operations for sum-of-products and 12 binary operation plus 8 unary operations for product-of-sums representation.  This shows the expressive power of AOP over Post. Thus, by no sense at all we can say that AOP is equivalent to Post.

Design Example-2.3:Using Orthogonal theorem-II

We use the same STAS system obtained by orthogonal theorem-I, but we substitute in orthogonal theorem-II to get the following.

F(A,B)= [A^{¾ D110}a B^{¾ D110}]a*[A^{¾ D110} a B^{¾ D210}]a*[A^{¾ D210} a B^{¾ D110}]a*[A^{¾ D212} a B^{¾ D212}]  

using AOP short-notations we get

F(A,B)= [A¹¹⁰a B¹¹⁰]a*[A¹¹⁰ a B²¹⁰]a*[A²¹⁰ a B¹¹⁰]a*[A²¹² a B²¹²]  

This representation uses 4 T4s and 3 T2s. That is a total of 7 binary operations and 8 orthogonal operators. 

Design Example-2.4: Smart Design Using AOP multi-operational set of basic operators

Using the multi-operational set of AOP, we can design this example by 3 binary operations and 2 unary operations.  A solution to this example, based on AOP multi-operators set, was carried out and gave 142 solutions. For example, we can design this example by using two T3's and T2 prioritors and three T5 conservative operators (solution#14). Thus AOP equation for this example is  f(A,B)=(AaB^¾f)m(A^¾fmB^¾f)  where a=T2, m=T3 and f=T5. This shows how AOP reduces circuit complexity of MVL circuits. Using the Image-Scaling theorem of AOP (a theorem in AOP that replaces DeMorgan's Laws),  we can go further and  reduce the number of conservative operators and get f(A,B)= (AaB^¾f)m(AbB)^¾fwhere b=T1.

Compare this design (3 binary operations & 2 unary operations) to Post representations (16 binary operations & 12 unary operations)!!!!!! 

Summary:
In the design of Example-2.1, we used the fundamental connectives of Post and obtained the given ternary operation as a composition of the basic connectives. What we got is a circuit with 16 binary operations and 12 unary operations for the sum-of-products representation and 20 binary operations and 16 unary operations for the product-of-sums. In the design of Example 2.2, we used the orthogonal theorem-I of AOP and its basic operators and we got 8 binary operations and 8 unary operations. In the design of Example 2.3, we used the orthogonal theorem-II of AOP and its basic operators and got a simpler circuit than the previous two designs with 7 binary operations and 8 unary operations. In the design of Example 2.42, we used 3 binary operations and 2 unary operations.

This shows that use of the new operators provides circuits that are more simpler and more efficient than use of the traditional operators.